Eric Weeks - personal pages - computer-generated pictures

Quasicrystals Page
[home] [research]
[software] [pics]
[misc/links] [about me]

weeks/physics.emory.edu

  1. Explanation
  2. Pictures
  3. Software
  4. Wallpaper
  5. Thanks
  6. Various Links

Explanation

Quasicrystals are tilings of the plane which are not periodic, but still can be symmetric. The most common form is called a Penrose tiling after the mathematician who invented it, and this tiling can have five-fold symmetry. These patterns can be generated typically by putting together two different tiles; a single tile alone will not work (for unusual symmetries, at least.)

Pictures

I have several pictures based on quasi-crystalline tiling. If you'd like to look at a gallery of all of my pictures, click on this text.

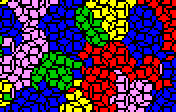
Here are clips from the pictures which specifically show quasi crystals; click to see the larger image.

Pictures of quasicrystals Cellular automata done on quasicrystals

Software

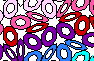
Click here to get a copy of the software that created this picture.

Quasicrystal wallpaper


 This is the image I am using as a background tile for this web page. It is cut from a larger image, below. In most browsers, if you right-click on the image at the right, you can download the tile.

Click here for more mathematical wallpaper tiles


This is made from a quasicrystalline tiling (a Penrose tiling). The fainter gray lines are the underlying tiling, consisting of fat and skinny diamonds. The black lines have been drawn by connecting the midpoints of the edges of the tiles. I have not connected all of the midpoints; if you look closely, you can see that the midpoints are connected between the edges extending from the obtuse angle of each tile. For the background tile of my home page (and this page), I clipped a symmetric region from this pattern.

The bars on this page are made from a similar sort of pattern.

Thanks to...

When I took Mike Marder's Solid State physics class, he assigned for homework the problem of generating a quasicrystalline tiling with a computer program. Ever since then I've been having fun making quasicrystal pictures. Later I went to the 8th Annual Complex Systems Summer School held at the Santa Fe Institute, where Dave Ardell suggested doing cellular automata on quasicrystals. This resulted in an additional burst of programming and many more pictures.

Current address:
Eric R. Weeks
weeks/physics.emory.edu
Department of Physics
Emory University
Atlanta, GA 30322-2430