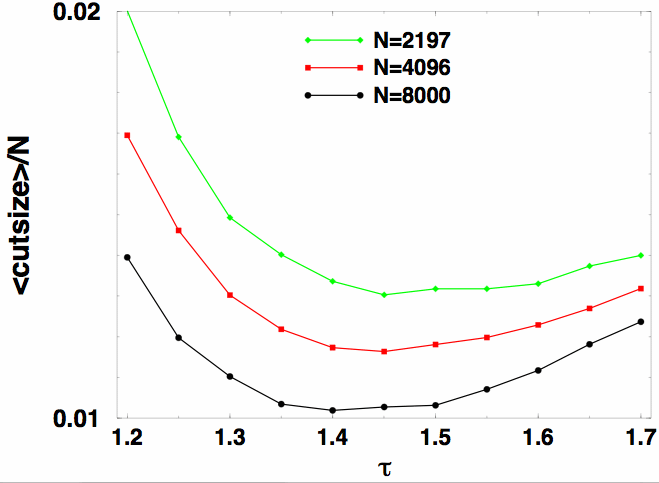
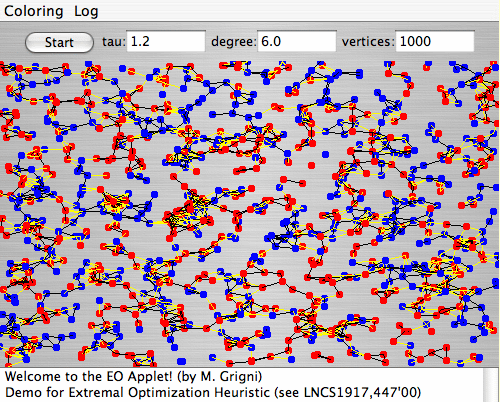
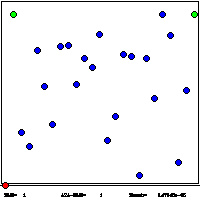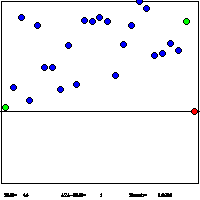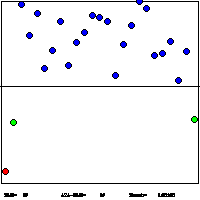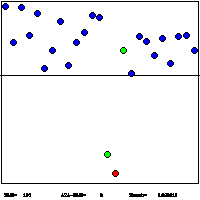
1. Extremal Optimization Demo for Graph Bi-Partitioning:

This Java applet demonstrates the behavior of τ-EO. In this variant of EO, a variable is chosen for an update according to a scale-free power-law distribution over the fitness rank k [ie. P(k)∼k ^-τ]. When τ >>1, only the lowest-ranked ("worst") variable with k=1 is updated, as described here. Such a local search often is too greedy, with update-activity much to localized on a few variables. If τ→0, variables are updated randomly and nothing is learned (not good!). Optimal behavior is obtained at intermediate values of τ (see Figure), where τ-EO maintains a strong bias to select low-ranked fitnesses (small k), but enough scale-free (non-equilibrium) fluctuations are induced to escape local minima.

GBP tries to partition the N vertices of a graph into two equal-sized (N/2) sets such that the number of edges between the two sets is minimal. Better heuristics than EO exist for this problem, based on the obvious clustering behavior of the vertices (see eg. METIS). Here, we don't even use clustering at start-up, using a random assignment instead, to get EO pure.

Lowest cost solutions found, averaged over a number of instances and EO-runs, as a function of τ for various graph sizes N. An optimal choice for τ emerges, which scales like τ-1∼1/log(N). Larger τ are too greedy, smaller τ are too random.

This applet was written by Mic Grigni:

Some things to try:

• Just click START and watch it go! ('Can be addictive for fans of the board game "Risk"!)
• Run EO first with τ=0.2 and notice that little progress is made in separating the two sets. There are many "bad" edges (in yellow). Then, change to τ=3.2 (and hit ↵!). Now, the cost ("cutsize") drastically decreases and segregation between red and blue vertices occurs. But soon the activity gets stuck, repeatedly moving the same variables without further gain. Finally, change to τ=1.2 and observe clustering, yet wide fluctuations in the interface. Slowly, the cutsize should further decrease. (Theory shows that τ-1∼1/log(N) for large N should be optimal for τ-EO.)
• Note: You can study a phase transition for the GBP by varying the average "degree" of vertices. For large n(!), there should always be a zero-cutsize solution for a degree <4.6, about.

2. Extremal Optimization Demo for Spin Glasses:

This Java applet also demonstrates the behavior of τ-EO, but for finding ground states of lattice spin glasses in d=2. (It also does Graph Partitioning for a dilute mesh; which corresponds to a bond-dilute ferromagnet fixed at zero magnetization!) The EO-algorithms is as described above. Again, there are much better, exact algorithms for this polynomial problem (see also the spin glass server in Köln), and EO distinguishes itself for spin glasses only for d >2. But problems in d >2 are harder to visualize.

Some things to try:

• Choose an odd system size (say, 39) and a small FM bond fraction (~0.02). You get a visible interface in the "fitness" view, pinned by the small bond disorder with (non-equilibrium) fluctuations depending on τ, similar to below.
• At size 40, make 0.5 FM bonds, set τ=0.5, then τ=3.5, τ=2.5, and τ=1.5, each time waiting until the "min. energy" plateaus. At high Bond Density, each change in τ improves the energy, but at least below 0.5 (=p_c), already the largest τ (most greedy!) should minimize the energy, since most energy "barriers" disappear.
• Set Bond Density 0.5 in "Graph" mode (ie. GBP) to get similar to the above.

3. Extremal Optimization Demo for SK-Spin Glasses:

This is a simple demo for the τ-EO algorithm described and used for the Sherrington-Kirkpatrick (SK) spin glass model. It's a monolithic C-program (last bug fix on 6/20/06) to download and compile with "gcc -O3 -lm demoSK.c -o demoSK.exe" or similar. Run "demoSK.exe" on any dumb terminal; it should be sufficiently clear (see Screenshot). The EO-algorithm uses (and displays) tree-ordered fitnesses, as first described here.

Some things to try:

• Just go with the defaults (and tap ↵)! Watch how the variables get reordered in the tree.
• Choose a larger system size (n<1024) and a fixed seed for bond disorder. Vary τ between runs, say, from 0.9-2.0. ( τ=1 exactly is singular!) See how the results vary with τ. (You should disable the configuration-output!)

EO for SK Demo:

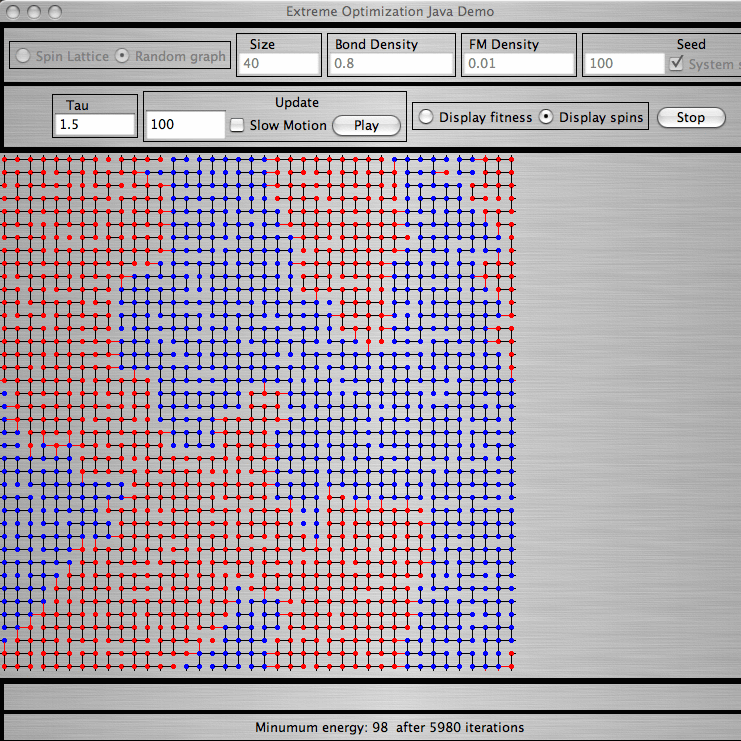
4. Extremal Optimization Demo for 2d Spin Glass:

This is a colorful demo of τ-EO on a 2d spin glass, similar to the above applet. Though, this is a monolithic C-program, eoglasspolt.c, for download and it requires the libraries in the "plotutils" package. (Works for me on Redhat/ Fedora, 'don't know about other platforms!) Compilation instructions are on first line of file. OK interface, but poorly documented.

Displayed on the lattice are merely the fitnesses of spins (from black=good to red=bad), not their orientation! Colors fade the longer a spin remains untouched.

Some things to try:

• Choose an odd system size (say, 99), T=1000000 updates and a small FM bond fraction (p+=0.02) for 0.5<τ<2.5, say. After some interesting coarsening phase, you get a visible interface, pinned by the small bond disorder with (non-equilibrium) fluctuations depending on τ. When τ is larger, the picture fades quickly everywhere to white except where the activity is localized. For about τ≈1.2, about, an optimal balance between greedy search and widely distributed activity is reached.

5. Bak-Sneppen Demo:

A simple program to demonstrate the Bak-Sneppen model of SOC, on which I have done some work. In particular, it has been the basis of the above Extremal Optimization (EO) heuristic. It consists of a lattice of uniform random numbers on [0,1] (=``fitnesses'' of species, say). Each time step, the smallest (``least fit'') number and its (``co-dependent'') neighbors are replace with new random numbers. A self-organized critical (SOC) state emerges with scale-free fluctuations and ``punctuated equilibrium''.

As above, this is a monolithic C-program, baksneppen.c, for download and it requires the libraries in the "plotutils" package. (Works for me on Redhat/ Fedora, 'don't know about other platforms!) Compilation instructions are on first line of file. The implementation is most primitive, but the animation may be interesting.

Funding:

Our work on disordered systems is currently supported by a DMR grant from the NSF. Another grant from the NSF has supported our research on Extremal Optimization. Computational equipment was purchased through a grant from the Emory University Research Council (URC), and start-up support. Previous partial support for Extremal Optimization was received from an LDRD-funded project at Los Alamos National Laboratory.