A little extra info

Energy can be minimized in different ways

The expression for the free energy of a system is:

E = U - TS (where U is the potential energy, T is the temperature and S is the entropy of the system)

As a system equilibrates it searches for the set of configurations that allows it to lower it's free energy the most. To minimize E at constant T there are two obvious choices:

1. The system can minimize its potential energy by placing each particle at the minimum of the potential energy surface created by the rest of the system. In practice, this often translates in placing a particle at a specified distance from its nearest neighbors and allowing small vibrations about that position.
2. The system can also try and maximize its entropy. This is in practice achieved by fluctuating between as many configurations as possible, usually while trying to maintain U as low as possible too.

Typically, at low temperatures, -TS is insufficient and the system opts to crystallize thus minimizing E mainly through a decrease in potential energy. This is all well and good most molecualr and atomic systems where the interparticle potential has well defined minima but for a hard sphere system such as our colloids, there are no suchminima and decreasing U is not an option.

At this point the system can only minimize free energy by maximizing entropy.

Entropy can be maximized by crystallizing!

Entropy is often naively misidentified as a measure of disorder. If this were the case then entropy maximization could hardly drive the transition from a disordered liquid to an ordered crystal!

In reality, entropy is related to Ω, the number of possible configurations a system can assume, by:

S = k_B ln(Ω) (where k_B is Boltzmann's constant)

So how does crystallization increase Ω? Consider a system of hard spheres that are random close-packed at Φ_rcp~63%. At this point all the particles are jammed against each other and cannot move. If you could take those same particles and container and crystallize the system, even partially, then you would optimize their packing and free up some volume (the maximum packing fraction for hard spheres is 74%). The newfound free volume would allow for all sorts of vibrations to occur and the number of vibrational configurations would increase drammatically.

The packing fraction of a tetrahedron

Volume of a regular tetrahedron of edge 2R is
V_tet = 2/3 R³√2
Dihedral angle of a tetrahedron is
θ = cos^-1(1/3) ~ 70.5 ^o ~ 0.3918π
Area of a sphere subtented by a tetrahedron with a vertex at the center of sphere is
A = (3x0.3918-1)R²π
Volume of the section of a sphere inside a regular tetrahedron, with a vertex at the sphere center is
V_sph = AR/3 = 0.05847R³

Tetrahdedral packing fraction is
4V_sph/V_tet ≈ 77.94%

Theorists like spin glasses

A spin glass is another glassy system that is frequently studied, often from a theoretical or computational point of view. Immagine a collection of spins (or compass needles) placed on a regular lattice. Here the disorder necessary to glassy dynamics is not in the spatial structure but in the randomness of the interactions between spins. Spin glass models can vary substantially in their details but they always require a mix of ferro- and antiferromagnetic interactions between spins, with spin pairs preferring an aligned or anti-aligned orientation respectively. At high temperatures, the spins do not feel the constraint of the interaction with their neighbors as much and are free to flip. As the temperature is lowered, the thermal energy E_thermal = k_BT cannot overcome the interaction between spins which becomes dominant.

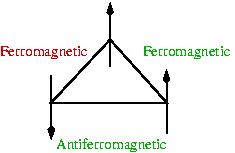Crucial to the formation of a spin glass is the presence of frustration. As you can see in the figure on the right, a closed loop with an odd number of antiferromagnetic interactions cannot have all "bonds" satisfied (green). The unsatisfied bond (red) can be shifted around by flipping one of the spins but cannot ever be satisfied. Of course this frustration gets much worse when there are n spins that interact with each other through a distribution of bonds...

To learn more about spin glasses you can go and talk to Stefan Boettcher or visit his website.