Clogging of soft particles
Xia Hong,
Dandan Chen,
Ken Desmond,
Piotr Habdas,
Anisa Hofert,
Yonglun Jiang,
Pablo Illing,
Meghan Kohne,
Ben Lonial,
Mia Morrell,
Ran Tao,
Haoran Wang,
Madelyn Wilson,
and Eric Weeks
Recent work in collaboration with
Corey O'Hern, Jack Treado, Yuxuan Cheng, Shivnag Sista, William Wang (Yale),
and Mark Shattuck (CCNY)
Lab Home --
People --
Experimental
facilities --
Publications
--
Experimental
pictures
-- Links
This page describes work published in:
- "Clogging of soft particles in 2D
hoppers"
X Hong, M Kohne, M Morrell, H Wang, & ER Weeks,
Phys. Rev. E 96, 062605 (2017).
- "Soft particle clogging in two-dimensional hoppers"
R Tao, M Wilson, & ER Weeks, Phys. Rev. E 104, 044909 (2021)
- "Clogging and avalanches in quasi-two-dimensional emulsion
hopper flow"
X Hong, KW Desmond, D Chen, & ER Weeks, Phys. Rev. E 105, 014603 (2022)
- "Hopper flows of deformable
particles"
Y Cheng, JD Treado, BF Lonial, P Habdas, ER Weeks, MD Shattuck,
and CS O'Hern, Soft Matter 18, 8071-8086 (2022)
- "Flow and clogging of capillary droplets"
Y Cheng, BF Lonial, S Sista, DJ Meer, A Hofert, ER Weeks, MD
Shattuck, and CS O'Hern, Soft Matter 20, 8036-8051 (2024).
Correction.
- Xia Hong dissertation
(2017) -- "Flow of quasi-two-dimensional emulsions: Clogging,
avalanches, and dynamics"
- Haoran Wang honors thesis
(2017) -- "Clogging of soft particles in a 2D hopper"
- Anisa Hofert honors thesis
(2020) -- "Flow of quasi-2D emulsion droplets through small openings"
- Ran Tao honors thesis
(2021) -- "Flow and clogging of soft particles in 2D hoppers"
- Ben Lonial honors thesis
(2021) -- "Dynamics of 2-dimensional soft particle flow through hopper"
Clogging occurs in a variety of situations: people exiting a crowded
room, particles passing through a filter, or corn exiting the bottom of
a silo. In general, you can think of clogging as occuring when
a dense collection of objects tries to leave a container through
a small opening. Often, there is a chance that the objects can
form an arch and block the ones behind them from exiting -- for example,
the glass marbles in the picture below.

(photo from Ran Tao.)
Clogging has been studied for decades, mostly by engineers who need
to understand solid particles flowing out of containers -- think corn,
coal, gravel, etc. Our work has focused on soft particles such as
oil droplets and hydrogel particles, as shown in the next two pictures:
| Picture at right: Oil
droplets forming clogs as they exit a funnel. The
droplets are between two parallel glass plates, so
they are deformed into pancakes. Click
here to see a movie of the clogging event shown in the
bottom row of images.
(Photos and video from Xia Hong.)
|

|
| Picture at right: Hydrogel
particles forming a clog. The particles are about 1.5 cm in diameter, and
the exit opening width is 2.88 cm. The apparatus is tilted so
that it is nearly horizontal to reduce
the driving force of gravity (10 degrees inclined from horizontal).
(Photo from Mia Morrell.)
|

|
|
Inspired by the
work of Kiwing To, Pik-Yin Lai, and H. K. Pak, we examine
the flow of these various types of particles as they drained
out of quasi-two-dimensional hoppers (the technical term
for these funnels shown in the pictures above). In all cases,
we control the opening size w and compare that to
the particle diameter d. If w/d is small, then
the system always clogs: the particles form an arch at the exit
and flow permanently stops. If w/d is large, then the
system never clogs: all the particles exit through the bottom.
For intermediate values of w/d, sometimes the system
clogs and sometimes not.
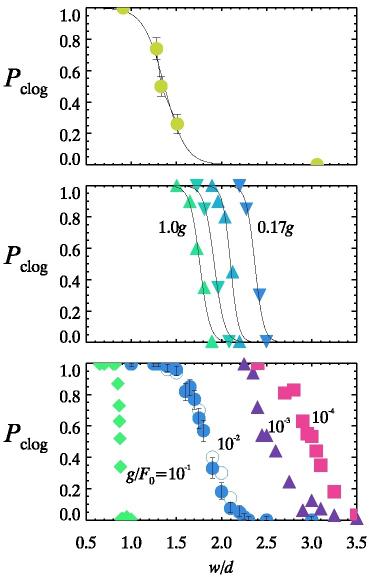
We do a bunch of experiments at different values of w/d and
measure the clogging probability, which leads to the graphs
shown at right. The top graph is for oil droplets: these rarely
clog, and require opening sizes less than about 1.5 times a
particle diameter to see clogging. The middle graph is for
hydrogel particles. We vary gravity by changing the tilt
of the experiment relative to vertical; the image below
shows Haoran tilting an older version of our sample chamber. For
a fully vertical experiment, it is harder to clog: this is the left-most
triangle symbols labeled 1.0g in the graph. For a nearly horizontal
experiment, it is much easier to clog: this is the right-most
curve labeled 0.17g in the graph.

|
|
The bottom graph shows our simulation data. We use
the
Durian
bubble model to simulate the flow of soft particles;
you can
click here to download our IDL code for these simulations.
Click here to see an animated
GIF movie of one of our
simulations. And this is a close-up movie
of the same data, with inter-droplet
forces highlighted. For these movies, w/d=2.2 and
the data correspond to the blue circles of the bottom clogging graph.
The simulation lets us vary gravity by three orders of magnitude. As
with the hydrogel particles, the lower the gravity, the easier it is
to clog -- we can get clogging even with large values of w/d, more
than three diameters wide.
The main idea here is that when gravity is big (or the particles are
very soft), the weight of the particles on top will make the
particles underneath deform. The soft particles can't form an arch, or
at least, if they try to form an arch, the weight causes that arch
to break. But when gravity is small (or the particles are harder),
it is easier to form a permanent arch that can support the weight
of the particles above it.
|
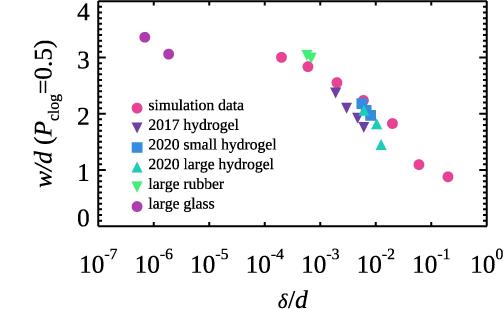
We need to see if the experiments and simulations are giving similar
results. To do this, we measure how much a single particle deforms
under its own weight. That's some distance delta, and we
divide that by the particle diameter d so that we have a
nondimensional quantity. We then determine the value of w/d for
which clogging occurs half the time for
each experiment or simulation, and plot that special value
of w/d as a function of delta/d. The
data are shown at right. The 2017 hydrogel data are from our 2017
paper (Hong et al), and the other data are from our 2021 paper (Tao et al).
|
|
What's fun about our results is that they are the exact opposite
of what people have seen for years with hard particles! With
hard particles, there's a phenomenon called "faster is slower."
This is easiest to understand with people trying to leave a crowded
room through a narrow doorway. If nobody is in a hurry, then people can
exit fairly efficiently. If people are rushing, then you can form
an arch of people at the doorway, and the crush of people from
behind can prevent the people in the arch from being able to move and
disrupt their arch. Thus, the flow of people out of the room
is actually slower than when people aren't in a hurry.
The key difference is that with people exiting a room,
they are moving somewhat randomly. If they form an arch, they're
going to continue to jostle each other to break free. And
if coal flows out of a container and gets stuck, you'll bang on
the container to break the clog. In this case, the
pressure of coal above will stabilize the arch against being
jostled by your banging on the container. In contrast,
with soft particles, we don't have random jostling or banging.
If a clog forms, it is stable. And instead, if we have
a larger driving force (larger gravity), this causes the
arch particles to deform and rearrange enough to break the
arch and flow will resume.
This does raise the question of whether adding vibrations to our
system will cause it to unclog. Mia Morrell did some experiments
showing that indeed this is the case, although we did not ever
see the "faster is slower" effect.
We did some additional experiments and simulations related to
flowing oil droplets. Briefly, in these cases we allowed the
pressure to build up if the system clogged, until the pressure
causes the arch to break, at which point the pressure drops.
Thus, we never had permanent clogs. Instead, we found that the
flow rate was intermittent, especially when we tried to pump
the droplets at low flow rates. In these cases we'd get a clog
followed by a big avalanche where many droplets flowed out.
When we tried to pump faster, the flow was steadier. We
were able to explain these results in terms of the system
compliance; see the 2022 paper by Xia Hong for details (link
at the top of this page).
For fun, here's a simulation picture where the clogging occured early on,
when the hopper was nearly full (almost 800 particles):
For more information, please contact
Eric Weeks <weeks(at)physics.emory.edu>


